Modular decoding: Scaling up by breaking down
There’s an unsung impasse currently facing commercially useful fault-tolerant quantum computers.
Useful quantum computers rely on quantum error-correcting codes that redundantly encode otherwise delicate logical information into a much larger system of physical qubits. But surprisingly, one of the pivotal bottlenecks for building a quantum device capable of implementing such codes is finding high accuracy, scalable, and fast classical decoding algorithms. The decoding algorithm is in a race against time to process the enormous amounts of data generated during a fault-tolerant quantum computation before logical information succumbs to errors. Without scalable and high throughput classical decoding algorithms, fault tolerance becomes impossible – a nail in the coffin for useful quantum computing.
That’s why we’re excited by our new modular decoding algorithm [1] – a world first scalable framework for real-time decoding, which will make it possible to run our first fault-tolerant machine.
A maze of measurements
There’s a lot going on during a fault-tolerant quantum computation. Although familiar operations like CNOTs and Hadamards innocuously take little space on a circuit diagram, implementing them fault tolerantly can involve thousands of measurements being performed on thousands of qubits over many clock cycles.
Visualizing the large volumes of measurement results generated by fault-tolerant operations (that a decoder must deal with) is most convenient in a logical blocks framework we recently introduced [2].
In this framework, we break down fault-tolerant implementations of familiar gates into the composition of a finite number of logical blocks. Each of these blocks is a specification of the spacetime locations of the many physical qubit operations required to perform fault-tolerant logical operations. The left-hand side of Figure 1 shows two sequential entangling, multi-qubit measurements represented in terms of logical blocks. Each block, demarcated by dashed lines, represents a large number of physical measurements to be performed – generating the vast amounts of classical data shown in the right-hand side of the figure.
Figure 1: A fault-tolerant quantum computation can be abstractly specified by a network of logical blocks stitched together in spacetime (left – as we describe in our logical blocks paper [2]). Each logical block involves numerous measurements, each generating binary data (right). A decoder needs to process gigabytes of this data every second, as the computation proceeds through the logical block network.
Decoders in detail
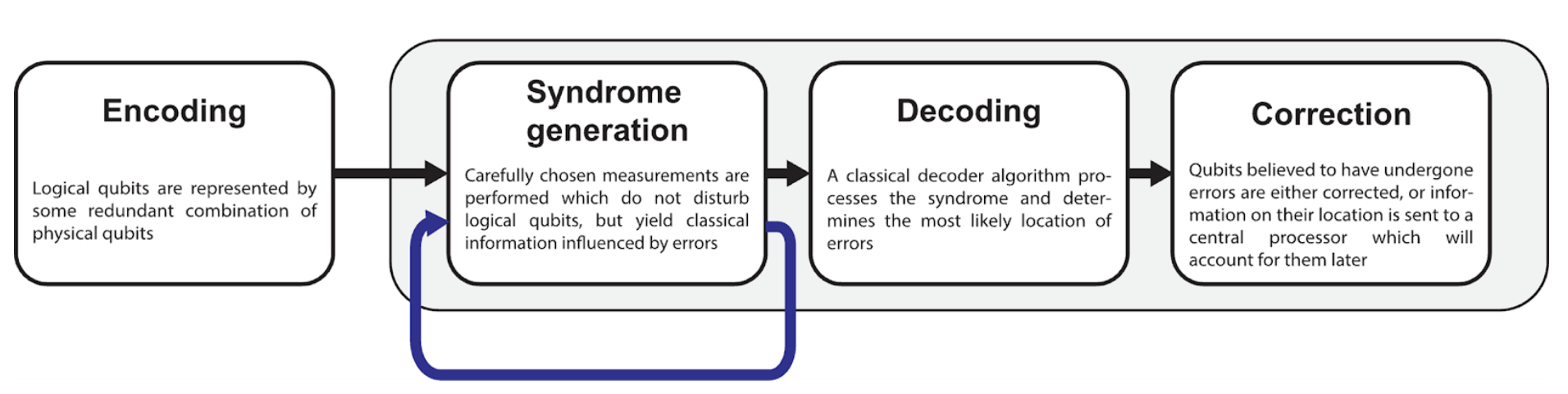
The decoder is tasked with processing the vast network of classical data shown on the right-hand side of Figure 1. Contained within this ever-growing volume of data is the error syndrome – a classical imprint of any errors that may have occurred on our qubits. Carefully studying the syndrome can allow us to infer where and when errors could have occurred to create the observed pattern of measurement results. This is the role of the classical decoding algorithm. It processes a syndrome, determines plausible locations of errors (in space and time), and decides the best way to compensate for them and produce fault-tolerant outcomes.
Figure 2 illustrates a simplified picture of how this process is continually repeated throughout a computation to keep errors in check and the computation on course. Even for early fault-tolerant machines, this relentless task typically requires the decoder to process Gigabytes of data every second per logical qubit. And there’s little room to trade precision for throughput – the accuracy of a decoding algorithm directly influences the reliability of a fault-tolerant quantum computer’s output. The quality of a classical decoder is just as important as the quality of the quantum hardware it supports!
Figure 2: Simplified viewpoint of the role of a decoder within a fault-tolerant quantum computation. Logical qubits are redundantly encoded in a quantum error-correcting code. Measurements, determined by a fault-tolerant protocol, are then repeatedly performed to generate a syndrome which is subsequently decoded to determine necessary corrections.
Throttled by throughput
Decoders need to be able to precisely process large amounts of data at the rate it is produced – in other words they need high throughput. This is critical, because on-the-fly decisions about how we proceed with a computation must consider information we expect from the decoder.
The reaction time is the time from when a given set of syndrome data is produced (for a certain logical operation or logical measurement outcome) to when the decoder returns its output. High reaction times do much more damage than just increasing our overall computer runtime. Waiting for a decoder means idling computational qubits – and idling qubits need error correction too. This generates even more syndrome information for the decoder to process. The result is a cascading backlog, and our computation quickly grinds to a halt without ever managing to produce useful output.
But things are worse still – even if we have a decoding algorithm with a very small reaction time, what happens when we add more logical qubits to our computer? Every additional logical qubit brings Gigabytes more syndrome data for the decoder to deal with, but it still needs to process it just as quickly. Since we need decoded logical outcomes in real-time, the decoder needs to process syndrome data at the rate it’s produced, no matter how much of it there is. There’s a lot written about the scalability of various quantum technologies, but classical decoders are a critical scaling challenge faced by all approaches.
As decoding algorithms will likely run on FPGA or ASIC hardware, it seems untenable that improvements in hardware will continually increase as quantum computing hardware grows.
Decoding piece by piece
Fortunately, there’s an algorithmic approach to solving this scalability problem – modular decoding. The essential idea is to break the problem into smaller pieces, which we can then parallelize on available decoder hardware. This means that scaling our fault-tolerant quantum computer requires decoder hardware to scale in space, not time. With modular decoding, larger decoder problems add more FPGAs or ASICs, rather than needing them to run faster.
But breaking down a quantum computation’s decoding into smaller sub-tasks is not trivial. Normally a decoder makes its deductions with access to the ‘whole syndrome’ created by measurements across all logical qubits. Can we maintain a high accuracy in estimating errors, if each decoder only gets a restricted view of some small part of the syndrome? We can, but it requires a few tricks.
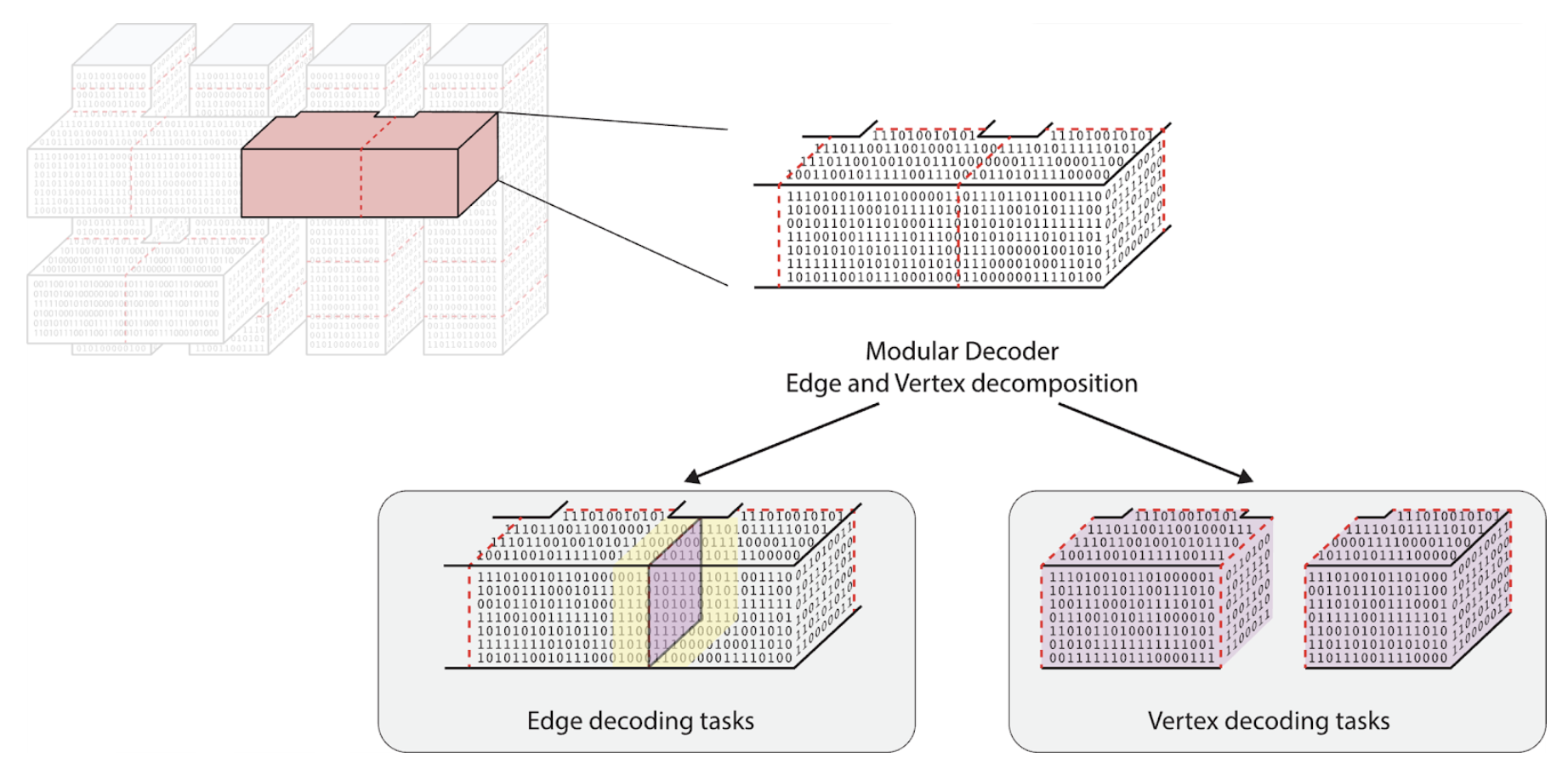
Firstly, we allow the many parallel decoders to communicate their outputs to each other. This means they can make decisions dependent on decoding results from neighboring areas of syndrome. The question is whether there is a way to structure the necessary communication such that it does not erode our parallelization improvements. Modular decoding achieves this using an edge-and-vertex decomposition of the error syndrome that we need our decoders to process. Informed by our logical blocks framework (see Figure 3), this methodology allows modular decoding to run a large number of decoders in parallel, with only manageable and scalable amounts of communication between them.
Figure 3: Example of how our modular decoder uses an edge and vertex decomposition to split up the decoding of logical blocks of syndrome data during a fault-tolerant quantum computation. The buffer region for edge decoding tasks is shown in yellow highlight.
Another trick is that we buffer some decoding tasks (shown with yellow highlight in the edge decoding task of Figure 3). This means that decoders working on these tasks receive more syndrome than is strictly necessary. Just how much buffering they receive can be tuned to fit the level of accuracy we require. While this extra information makes each decoding task longer to compute, we show that this small additional window of information makes a crucial difference in accuracy.
It’s not obvious that the divide and conquer strategy of modular decoding is truly scalable. What if the required communication between decoders becomes a bottleneck for larger computations? In [1] we address this, showing analytically that the decoders’ performance can be maintained. We also implement and benchmark modular decoding within several relevant simulations of large-scale fault-tolerant computations. These include first-of-its kind simulations of magic-state distillation, one of the most ubiquitous and costly subroutines in fault-tolerant quantum computing. These simulations also show that scalable real-time modular decoding incurs no loss in accuracy.
We’re confident and excited that modular decoding meets all the practical requirements necessary to enable useful, fault-tolerant quantum computing.
Bibliography
[1] H. Bombín, C. Dawson, Y.-H. Liu, N. Nickerson, F. Pastawski, and S. Roberts, Modular Decoding: Parallelizable Real-Time Decoding for Quantum Computers, arXiv:2303.04846.
[2]H. Bombin, C. Dawson, R. V. Mishmash, N. Nickerson, F. Pastawski, and S. Roberts, Logical Blocks for Fault-Tolerant Topological Quantum Computation, arXiv:2112.12160.